Phân cụm K-Means

Thuật toán K-Means là một trong những thuật toán học không giám sát (Unsupervised Learning) phổ biến nhất để phân cụm (clustering) dữ liệu. Thuật toán này chia dữ liệu thành K nhóm (clusters) sao cho các điểm dữ liệu trong cùng một cụm có đặc điểm tương đồng nhau.

Một số ứng dụng như phân cụm khách hàng theo hành vi mua hàng, phân nhóm ảnh theo đặc điểm màu sắc, nhóm tài liệu có nội dung tương tự.

Thuật toán K-Means hoạt động theo các bước sau:

1. Chọn số lượng cụm K: Người dùng cần xác định trước số lượng cụm mong muốn.
2. Khởi tạo tâm cụm (centroids): Chọn ngẫu nhiên K điểm làm tâm ban đầu của các cụm.
3. Phân loại điểm dữ liệu:
   • Mỗi điểm dữ liệu được gán vào cụm có tâm gần nhất (dựa trên khoảng cách Euclidean).
4. Cập nhật tâm cụm:
   • Tính trung bình tất cả các điểm trong mỗi cụm để cập nhật tâm cụm mới.
5. Lặp lại quá trình (Bước 3 & 4):
   • Quá trình này tiếp tục cho đến khi tâm cụm không thay đổi hoặc số vòng lặp đạt giới hạn.

Khoảng cách Euclidean giữa hai điểm A(x1,y1) và B(x2,y2) được tính như sau:

 Cho bài toán như sau:

Giả sử chúng ta có danh sách khách hàng với thu nhập hàng tháng và  và chi tiêu hàng tháng (triệu đồng). Mục tiêu là phân chia khách hàng thành 3 nhóm dựa trên hành vi chi tiêu. Cách thức giải như sau:

Bước 1: Tạo dữ liệu mẫu:

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.cluster import KMeans

from sklearn.preprocessing import StandardScaler

# Dữ liệu thu nhập và chi tiêu

data = {

    'Thu nhập (triệu đồng)': [15, 16, 17, 30, 31, 32, 60, 61, 62, 100, 101, 102],

    'Chi tiêu (triệu đồng)': [40, 42, 45, 60, 62, 65, 90, 91, 95, 120, 121, 125]

}

# Chuyển dữ liệu thành DataFrame

df = pd.DataFrame(data)

Bước 2: Tiền xử lý dữ liệu

# Huấn luyện scaler mà không sử dụng tên cột

scaler = StandardScaler()

scaler.fit(df[['Thu nhập (triệu đồng)', 'Chi tiêu (triệu đồng)']].values)

df_scaled = scaler.fit_transform(df)

Bước 3: Áp Dụng K-Means

 # Áp dụng thuật toán K-Means với K=3

kmeans = KMeans(n_clusters=3, random_state=42)

df['Cụm'] = kmeans.fit_predict(df_scaled)

# Lấy tâm cụm

centroids = kmeans.cluster_centers_

Bước 4: Dự đoán giá trị mới

# Dữ liệu mới

new_data = np.array([[50, 70]])

# Chuẩn hóa dữ liệu mới

new_data_scaled = scaler.transform(new_data)

# Dự đoán cụm

cluster = kmeans.predict(new_data_scaled)

print(f'Khách hàng mới thuộc cụm số: {cluster[0]}')

Bước 5: Vẽ Biểu Đồ Phân Cụm

plt.figure(figsize=(8,6))

# Vẽ điểm dữ liệu theo cụm

plt.scatter(df['Thu nhập (triệu đồng)'], df['Chi tiêu (triệu đồng)'], c=df['Cụm'], cmap='viridis', s=100, label='Khách hàng')

# Vẽ tâm cụm

plt.scatter(scaler.inverse_transform(centroids)[:, 0], scaler.inverse_transform(centroids)[:, 1], 

            c='red', marker='X', s=200, label='Tâm cụm')

plt.xlabel('Thu nhập (triệu đồng)')

plt.ylabel('Chi tiêu (triệu đồng)')

plt.title('Phân Cụm Khách Hàng với K-Means')

plt.legend()

plt.show()

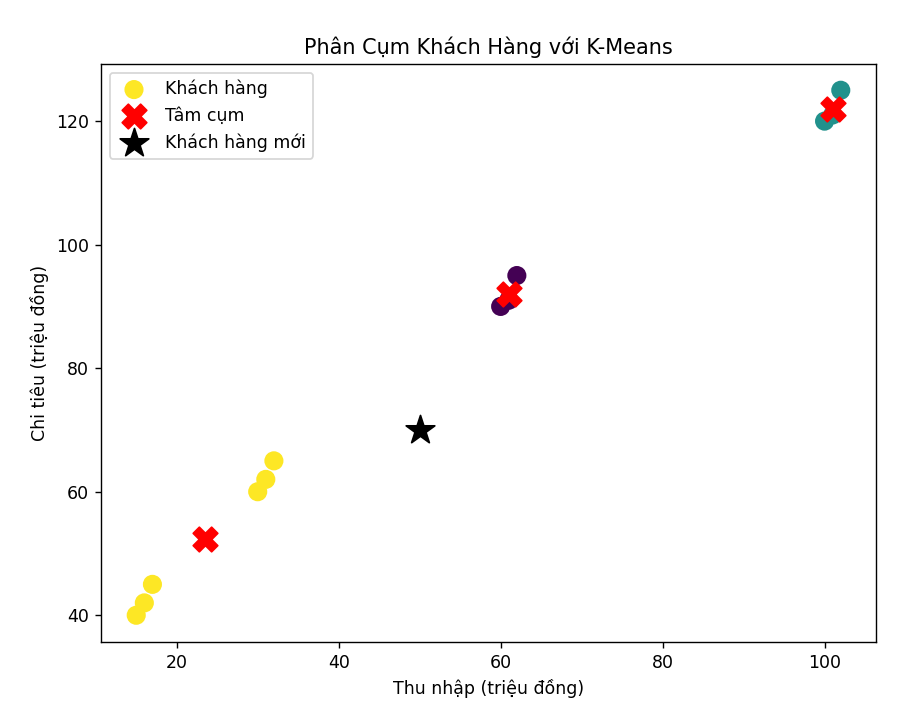
Ảnh 4‑2: Kết quả của quá trình huấn luyện và phân cụm

Một vấn đề quan trọng của K-Means là cần chọn giá trị K phù hợp tức có bao nhiêu cụm. Chúng ta sử dụng phương pháp Elbow để tìm giá trị K tốt nhất.

wcss = []

for k in range(1, 10):

    kmeans = KMeans(n_clusters=k, random_state=42)

    kmeans.fit(df_scaled)

    wcss.append(kmeans.inertia_)  # Tổng bình phương khoảng cách nội cụm

# Vẽ biểu đồ Elbow

plt.plot(range(1, 10), wcss, marker='o', linestyle='--')

plt.xlabel('Số cụm K')

plt.ylabel('WCSS (Within-cluster sum of squares)')

plt.title('Phương pháp Elbow')

plt.show()

Từ đồ thị cho thấy K tối ưng là bằng 4.

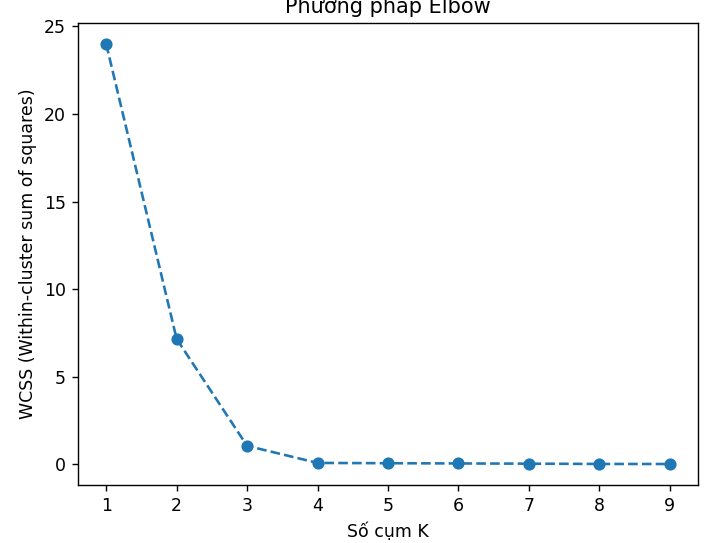
Ảnh 4‑3: Biểu đồ thể hiện Tổng bình phương khoảng cách nội cụm trên từng số cụm khác nhau.

Trong thực tế K-Means được sử dụng trong các ứng dụng Phân cụm khách hàng (Customer Segmentation). Ví dụ nhóm khách hàng theo hành vi mua hàng để tối ưu hóa chiện lược marketing, nhận diện nhóm khách hàng tiềm năng. Ngoài ra dùng trong phân nhóm ảnh, phát hiện bất thường (trong giao dịch khách hàng, lỗi trong sản xuất), phân cụm văn bản (tạo nhóm tài liệu có nội dung tương tự, tìm kiếm và gợi ý tin tức).

Ưu điểm của K-Means là dễ hiểu, dễ triển khai, hiệu suất nhanh, phù hợp với dữ liệu lớn, và có thể ứng dụng rộng rãi trên nhiều lĩnh vực. Nhược điểm của nó là cần chọn số lượng cụm K trước (không tự động tối ưu), nhạy cảm với tâm cụm ban đầu, có thể cho kết quả khác nhau mỗi lần chạy, hoạt động kém với dữ liệu không có dạng cụm hình cầu (clusters không có biên rõ ràng).