Bài toán mê cung và tìm đường đi ngắn nhất

Bài toán mê cung là một trong những bài toán tìm kiếm điển hình trong trí tuệ nhân tạo. Nó mô phỏng một hệ thống gồm các lối đi có chướng ngại vật, nơi mà một tác nhân cần tìm ra con đường tối ưu từ vị trí xuất phát đến đích. 

Cho một mê cung được biểu diễn dưới dạng một ma trận hoặc đồ thị, trong đó mỗi ô hoặc nút đại diện cho một vị trí. Một số vị trí là tường hoặc chướng ngại vật, không thể di chuyển qua. Mục tiêu là tìm đường đi từ điểm bắt đầu đến điểm đích sao cho tổng số bước hoặc chi phí di chuyển là nhỏ nhất.

Một số khái niệm quan trọng trong bài toán:

• Không gian trạng thái: là tập hợp tất cả các vị trí mà tác nhân có thể đi đến.
• Toán tử trạng thái: Các phép di chuyển lên, xuống, trái, phải hoặc chéo tùy vào quy tắc của bài toán.
• Hàm đánh giá: Xác định khoảng cách từ trạng thái hiện tại đến đích (có thể sử dụng heuristic trong thuật toán tìm kiếm).

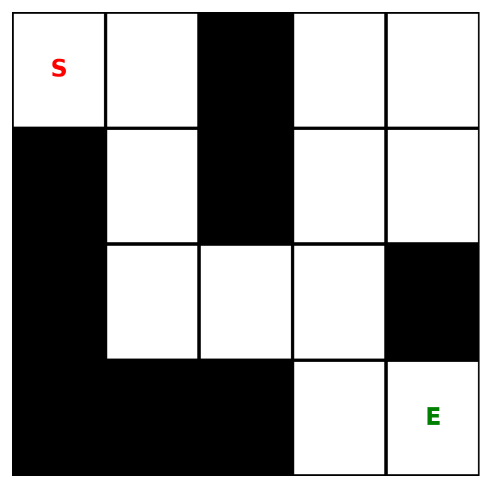
Ảnh 3‑1: Hình ảnh mê cung

Ví dụ cho một mê cung như ảnh 3-1. Các ô đen là tường, các ô trắng là đường đi. Điểm bắt đầu là S và điểm kết thúc là điểm E. Biễu diễn mê cung trên thành một ma trận nhị phân trong đó 0 biểu thị ô không thể đi qua và 1 biễu thị ô có thể đi qua.

1        1        0        1        1

0        1        0        1        1

0        1        1        1        0

0        0        0        1        1

Các thuật toán giải quyết bài toán mê cung là tìm kiếm theo chiều sâu (Depth-First Search – DFS), tìm kiếm theo chiều rộn (Breadth-First Search – BFS), thuật toán Dijkstra, và A*.

Mê cung thực chất là một đồ thị 2D mà trong đó mỗi ô có thể đi qua (1) là một đỉnh (node), mỗi đường đi hợp lệ giữa hai ô là một cạnh (edge). 

Có hai cách phổ biến để biểu diễn đồ thị, ma trận kề (Adjacency Matrix) và danh sách kề (Adjacency List). Ma trận kề cần O(N²) bộ nhớ để lưu trữ tất cả các đỉnh, ngay cả khi một số đỉnh không có kết nối. Danh sách kề chỉ lưu các cạnh thực tế, giúp tiết kiệm bộ nhớ đáng kể khi đồ thị có ít cạnh (đồ thị thưa). Giả sử mê cung có 10.000 ô, nhưng chỉ có 10% ô có thể đi qua thì ma trận kề sẽ tốn quá nhiều bộ nhớ, trong khi danh sách kề chỉ lưu các kết nối hợp lệ. Sử dụng danh sách kề giúp tìm kiếm nhanh hơn khi áp dụng các thuật toán như DFS, BFS, Dijkstra hay A*.

Để tìm danh sách kề từ ma trận của mê cung, ta cần tìm danh sách kề theo ý tưởng sau: duyệt qua từng ô trong ma trận, nếu ô là 1, kiểm tra các ô hàng xóm( ô lân cận) của nó (trên, dưới, trái phải). Nếu ô hàng xóm là 1 thì thêm cạnh vào danh sách kề. Dưới đây là code tìm danh sách kề:

def generate_adjacency_list(maze):

    rows, cols = len(maze), len(maze[0])

    adjacency_list = {}  # Khởi tạo danh sách kề

    directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]  # Lên, Xuống, Trái, Phải

    # Đánh số mỗi ô có thể đi (1) theo thứ tự duyệt từ trên xuống dưới, trái sang phải

    node_mapping = {}

    node_id = 0

    for i in range(rows):

        for j in range(cols):

            if maze[i][j] == 1:

                node_mapping[(i, j)] = node_id

                adjacency_list[node_id] = []

                node_id += 1

    # Tạo danh sách kề

    for (i, j), node in node_mapping.items():

        for dx, dy in directions:

            ni, nj = i + dx, j + dy

            if (ni, nj) in node_mapping:  # Nếu hàng xóm hợp lệ

                adjacency_list[node].append(node_mapping[(ni, nj)])

    return adjacency_list

# Mê cung đầu vào (1: đường đi, 0: tường)

maze = [

    [1, 1, 0, 1, 1],

    [0, 1, 0, 1, 1],

    [0, 1, 1, 1, 0],

    [0, 0, 0, 1, 1]

]

# Tạo danh sách kề

adj_list = generate_adjacency_list(maze)

# Hiển thị danh sách kề

for node, neighbors in adj_list.items():

    print(f"{node}: {neighbors}")

 Kết quả của code trên là:

Ảnh 3‑2: Kết quả tìm danh sách kề

Danh sách kề này là dữ liệu đầu vào cho các thuật toán tìm kiếm.

3.1.2. Thuật toán tìm theo chiều sâu DFS

Tìm kiếm theo chiều sâu (DFS) là một thuật toán duyệt hoặc tìm kiếm trên đồ thị bằng cách đi sâu vào một nhánh trước khi quay lại để kiểm tra các nhánh khác. Nó có thể được triển khai bằng đệ quy hoặc bằng ngăn xếp (stack).

Trong bài toán mê cung, DFS có thể tìm ra một đường đi từ điểm S (Start) đến E (End), nhưng không đảm bảo đó là đường đi ngắn nhất. Thuật toán này thường được dùng vào tìm đường trong mê cung, duyệt cây hoặc đồ thị để kiểm tra kết nối, tìm tất cả các thành phần liên thông trong một đồ thị.

DFS hoạt động dựa trên nguyên tắc LIFO (Last In, First Out), có thể triển khai bằng:

• Đệ quy: Dùng ngăn xếp của hệ thống để lưu trạng thái.
• Ngăn xếp tường minh: Dùng stack để kiểm soát các bước di chuyển.

Giả sử đồ thị được biểu diễn dưới dạng danh sách kề thì các bước thực hiện như sau:

• Bắt đầu từ một đỉnh (start node).
• Đánh dấu đỉnh đó là đã thăm.
• Duyệt tất cả các đỉnh kề:
  • Nếu đỉnh kề chưa được thăm → gọi DFS trên đỉnh đó.
  • Nếu đã thăm → bỏ qua.
• Quay lui (backtracking) khi không còn đỉnh nào để duyệt.

Đồ thị được vẽ ra từ ma trận mê cung ở phần 3.1.1:

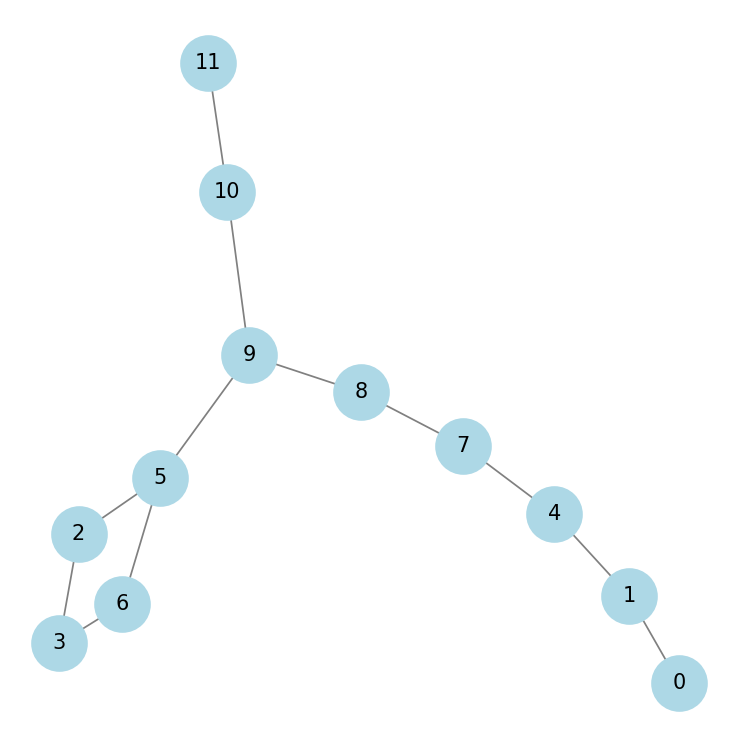
Ảnh 3‑3: Đồ thị dược vẽ từ danh sách kề của ma trận nhị phân mê cung

Dưới đây là code vẽ đồ thị:

import networkx as nx

import matplotlib.pyplot as plt

def draw_maze_graph(adjacency_list):

    """Vẽ đồ thị từ danh sách kề của mê cung."""

    G = nx.Graph()

    # Thêm cạnh vào đồ thị

    for node, neighbors in adjacency_list.items():

        for neighbor in neighbors:

            G.add_edge(node, neighbor)

    # Tạo bố cục cho đồ thị

    pos = nx.spring_layout(G)

    # Vẽ đồ thị

    plt.figure(figsize=(6, 6))

    nx.draw(G, pos, with_labels=True, node_color="lightblue", edge_color="gray", node_size=1000, font_size=12)

    plt.title("Đồ thị biểu diễn mê cung")

    plt.show()

# Danh sách kề của mê cung

maze_graph = {

    0: [1],

    1: [0, 4],

    2: [3, 5],

    3: [2, 6],

    4: [1, 7],

    5: [2, 6, 9],

    6: [3, 5],

    7: [4, 8],

    8: [7, 9],

    9: [5, 8, 10],

    10: [9, 11],

    11: [10]

}

# Gọi hàm vẽ đồ thị

draw_maze_graph(maze_graph)

Ứng với bài toán của chúng ta, vị trí bắt đầu là nút 0 và lối ra là nút 11. Thuật toán được sử dụng đệ quy và stack được biễu diễn dưới dạng mã giả.

HÀM DFS_Đệ_Quy(đồ_thị, đỉnh, đã_thăm)

    NẾU đỉnh KHÔNG thuộc đã_thăm THÌ

        ĐÁNH DẤU đỉnh là đã thăm

        HIỂN THỊ đỉnh 

        CHO MỖI đỉnh_kề trong đồ_thị[đỉnh] LÀM

            DFS_Đệ_Quy(đồ_thị, đỉnh_kề, đã_thăm)

    KẾT THÚC NẾU

KẾT THÚC HÀM

HÀM DFS_Stack(đồ_thị, đỉnh_bắt_đầu)

    TẠO một NGĂN_XẾP rỗng

    ĐẨY đỉnh_bắt_đầu vào NGĂN_XẾP

    TẠO một tập HỢP đã_thăm rỗng

    LẶP KHI NGĂN_XẾP KHÔNG rỗng

        LẤY RA đỉnh ← POP từ NGĂN_XẾP

        NẾU đỉnh KHÔNG thuộc đã_thăm THÌ

            ĐÁNH DẤU đỉnh là đã thăm

            HIỂN THỊ đỉnh  // Xử lý đỉnh hiện tại

            CHO MỖI đỉnh_kề trong đồ_thị[đỉnh] THEO THỨ TỰ ĐẢO NGƯỢC LÀM

                ĐẨY đỉnh_kề vào NGĂN_XẾP

    KẾT THÚC LẶP

KẾT THÚC HÀM

Cài đặt thuật toán đệ quy và stack trong python như sau:

def dfs_de_quy(graph, node, visited):

    """DFS đệ quy để duyệt mê cung."""

    if node not in visited:

        print(node, end=" ")

        visited.add(node)

        for neighbor in graph[node]:

            dfs_de_quy(graph, neighbor, visited)

def dfs_stack(graph, start):

    """DFS sử dụng ngăn xếp để duyệt mê cung."""

    visited = set()

    stack = [start]

    while stack:

        node = stack.pop()

        if node not in visited:

            print(node, end=" ")

            visited.add(node)

            stack.extend(reversed(graph[node]))

def main():

    # Danh sách kề của mê cung

    maze_graph = {

        0: [1],

        1: [0, 4],

        2: [3, 5],

        3: [2, 6],

        4: [1, 7],

        5: [2, 6, 9],

        6: [3, 5],

        7: [4, 8],

        8: [7, 9],

        9: [5, 8, 10],

        10: [9, 11],

        11: [10]

    }

    print("DFS Đệ Quy:")

    visited_set = set()

    dfs_de_quy(maze_graph, 0, visited_set)

    print("\nDFS Dùng Ngăn Xếp:")

    dfs_stack(maze_graph, 0)

Kết quả của chương trình: 

Ảnh 3‑4: Kết quả của thuật toán DFS cài đặt trên đệ quy và ngăn xếp

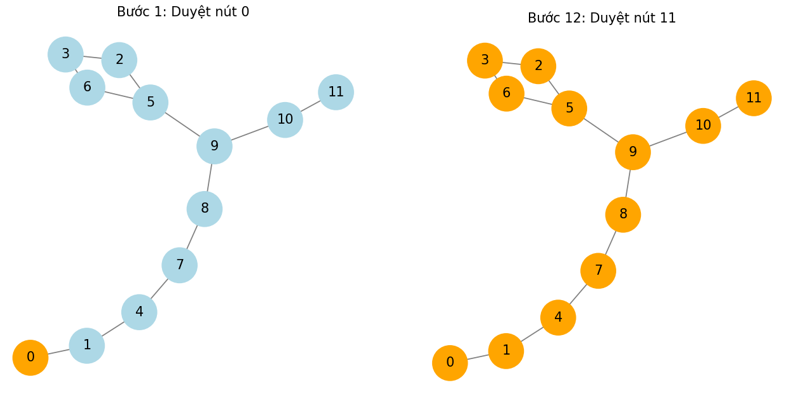
Ảnh 3‑5: Ví dụ duyệt qua các nút

3.1.3. Thuật toán tìm theo chiều rộng (BFS)

BFS (Breadth-First Search) là một thuật toán tìm kiếm trên đồ thị hoặc cây, hoạt động theo chiều rộng. Thay vì đi sâu vào một nhánh như DFS, BFS sẽ duyệt theo từng mức trước khi mở rộng sang các đỉnh kế tiếp. 

Nguyên lý hoạt động của BFS là duyệt từ gốc (start), thăm tất cả các đỉnh kề của nó trước, sau đó, tiếp tục mở rộng các đỉnh ở mức tiếp theo theo thứ tự FIFO (First In, First Out) bằng hàng đợi (Queue). BFS đảm bảo tìm được đường đi ngắn nhất trong đồ thị không trọng số.

Các bước thực hiện thuật toán BFS:

• Khởi tạo hàng đợi (queue) với đỉnh bắt đầu.
• Tạo tập hợp đã thăm (visited) để lưu các đỉnh đã được duyệt.
• Lặp lại các bước sau đến khi hàng đợi rỗng:
  • Lấy đỉnh đầu tiên trong hàng đợi.
  • Thêm các đỉnh kề của nó vào hàng đợi (nếu chưa được thăm).
• Nếu gặp đỉnh đích (end), dừng lại.

Mã giả của thuật toán BFS:

HÀM BFS(đồ_thị, đỉnh_bắt_đầu):

    Tạo HÀNG_ĐỢI (queue) và thêm đỉnh_bắt_đầu vào

    Tạo danh sách đã_thăm

     LẶP KHI HÀNG_ĐỢI KHÔNG rỗng:

        LẤY đỉnh hiện tại từ HÀNG_ĐỢI

        NẾU đỉnh hiện tại là đỉnh đích:

            TRẢ VỀ đường đi

        THÊM đỉnh hiện tại vào danh sách đã_thăm

        CHO MỖI đỉnh_kề của đỉnh hiện tại:

            NẾU đỉnh_kề chưa được thăm:

                THÊM đỉnh_kề vào HÀNG_ĐỢI

                LƯU đường đi

    TRẢ VỀ "Không tìm thấy đường đi"

Cài đặt BFS trong python:

from collections import deque

def bfs_find_path(graph, start, end):

    """BFS tìm đường đi ngắn nhất từ điểm bắt đầu đến điểm kết thúc."""

    queue = deque([(start, [start])])  # Hàng đợi lưu trạng thái (node, path)

    visited = set()

    while queue:

        node, path = queue.popleft()

        if node == end:

            return path  # Trả về đường đi nếu tìm thấy

        if node not in visited:

            visited.add(node)

            for neighbor in graph[node]:

                if neighbor not in visited:

                    queue.append((neighbor, path + [neighbor]))

    return None  # Không tìm thấy đường đi

Kết quả của thuật toán là: [0, 1, 4, 7, 8, 9, 10, 11]

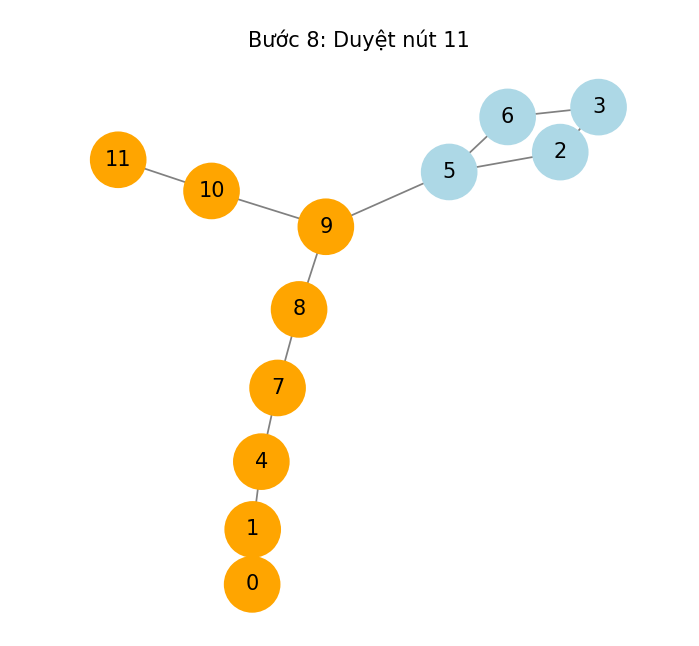
Ảnh 3‑6: Hình ảnh tìm đường đi theo thuật toán BFS

3.1.4. Bài toán tìm đường đi ngắn nhất với giải thuật Dijkstra

Thuật toán Dijkstra là một thuật toán nổi tiếng dùng để tìm đường đi ngắn nhất từ một đỉnh nguồn đến các đỉnh khác trong đồ thị có trọng số không âm. Điểm nổi bật của Dijkstra:

• Dùng hàng đợi ưu tiên để mở rộng các đỉnh có khoảng cách ngắn nhất trước.
• Không hoạt động với trọng số âm, nhưng hoạt động hiệu quả với đồ thị không trọng số và có trọng số dương.
• Tìm được đường đi ngắn nhất từ một đỉnh đến tất cả các đỉnh khác.

Dijkstra sử dụng một hàng đợi ưu tiên (priority queue) để chọn đỉnh gần nhất và mở rộng nó.

Các bước thực hiện thuật toán:

1. Khởi tạo khoảng cách từ đỉnh bắt đầu đến tất cả các đỉnh là vô cực (∞), riêng đỉnh bắt đầu có khoảng cách = 0.
2. Đưa đỉnh bắt đầu vào hàng đợi ưu tiên (ưu tiên đỉnh có khoảng cách ngắn nhất).
3. Trong khi hàng đợi chưa rỗng:

• Lấy ra đỉnh có khoảng cách nhỏ nhất từ hàng đợi.
• Duyệt tất cả đỉnh kề và cập nhật khoảng cách nếu tìm được đường đi ngắn hơn.
• Thêm các đỉnh được cập nhật vào hàng đợi ưu tiên.

1. Khi tìm thấy đỉnh đích, truy vết lại đường đi từ đích về nguồn.

Mã giả của thuật toán:

HÀM Dijkstra(đồ_thị, đỉnh_bắt_đầu):

    Tạo hàng đợi ưu tiên (priority_queue)

    Khởi tạo khoảng cách của tất cả các đỉnh = ∞, riêng đỉnh_bắt_đầu = 0

    Đưa (đỉnh_bắt_đầu, 0) vào hàng đợi

    Trong khi hàng đợi KHÔNG rỗng:

        LẤY đỉnh hiện tại có khoảng cách nhỏ nhất

        NẾU đỉnh hiện tại là đỉnh đích:

            TRẢ VỀ đường đi

        CHO MỖI đỉnh_kề của đỉnh hiện tại:

            TÍNH khoảng cách mới

            NẾU khoảng cách mới NHỎ HƠN khoảng cách cũ:

                CẬP NHẬT khoảng cách

                ĐƯA vào hàng đợi

    TRẢ VỀ "Không tìm thấy đường đi"

Với bài toán tìm đường đi trong mê cung, coi trọng số của mỗi ô đi qua ô khác là 1, ta có thể tạo ra đồ trị trọng số từ mê cung bằng cách mở rộng hàm tìm danh sách kề.

def generate_weighted_graph(maze):

    """Chuyển ma trận mê cung thành đồ thị trọng số."""

    rows, cols = len(maze), len(maze[0])

    graph = {}  # Đồ thị trọng số

    node_mapping = {}  # Ánh xạ (i, j) -> node_id

    node_id = 0

    # Đánh số các ô có thể đi

    for i in range(rows):

        for j in range(cols):

            if maze[i][j] == 1:

                node_mapping[(i, j)] = node_id

                graph[node_id] = []

                node_id += 1

    # Tạo danh sách kề với trọng số

    directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]  

    for (i, j), node in node_mapping.items():

        for dx, dy in directions:

            ni, nj = i + dx, j + dy

            if (ni, nj) in node_mapping:

                graph[node].append((node_mapping[(ni, nj)], 1))  

    return graph, node_mapping

Kết quả của hàm này ta có:

Ảnh 3‑7: Kết quả tạo danh sách kề có trọng số

Từ kết quả trên ta thấy đỉnh 1 kề với đỉnh 0 và 4 và có trọng số là 1. Tương tự như các đỉnh khác. Với các bài toán khác, trọng số có thể thay đổi tùy thuộc bài toán.

Cài đặt hàm tìm kiếm Dijkstra trong python như sau:

def dijkstra(graph, start, end):

    """Dijkstra tìm đường đi ngắn nhất từ start đến end trong đồ thị có trọng số."""

    priority_queue = []

    heapq.heappush(priority_queue, (0, start, [start]))  # (khoảng cách, đỉnh, đường đi)

    shortest_distances = {node: float('inf') for node in graph}

    shortest_distances[start] = 0

    while priority_queue:

        current_distance, current_node, path = heapq.heappop(priority_queue)

        if current_node == end:

            return path, current_distance  # Trả về đường đi và khoảng cách

        for neighbor, weight in graph[current_node]:

            distance = current_distance + weight

            if distance < shortest_distances[neighbor]:

                shortest_distances[neighbor] = distance

                heapq.heappush(priority_queue, (distance, neighbor, path + [neighbor]))

    return None, float('inf')  # Không tìm thấy đường đi

Kết quả của chương trình ta có:

Ảnh 3‑8: Kết quả của thuật toán Dijkstra

Ảnh 3‑9: Hình ảnh mô phỏng quá trình thực hiện thuật toán Dijkstra

Hàm Dijkstra thường được dùng trong việc tìm đường đi ngắn nhất với trọng số không đông đều. Trong AI thuật toán này thường được dùng để trong game hoặc robot.