Bài toán hồi quy tuyến tính

 Hồi quy tuyến tính

Hồi quy tuyến tính (Linear Regression) là một trong những thuật toán học có giám sát (Supervised Learning) được sử dụng phổ biến trong dự đoán giá trị liên tục. Thuật toán này xây dựng một mô hình để tìm mối quan hệ giữa một hoặc nhiều biến đầu vào (biến độc lập) với biến đầu ra (biến phụ thuộc) bằng cách sử dụng một đường thẳng tốt nhất. 

Hồi quy tuyến tính tìm cách biểu diễn mối quan hệ giữa biến đầu vào x và biến đầu ra y bằng phương trình:

Trong đó:

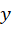• là giá trị dự đoán (output).
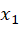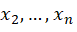• , là các biến đầu vào (features).
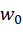• là hằng số chặn (Intercept – Bias).
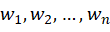• ​ là các hệ số hồi quy (Weights).
• ϵ là sai số (Noise), thể hiện mức độ sai lệch giữa giá trị thực tế và giá trị dự đoán.

Có hai dạng chính của hồi quy tuyến tính hồi quy tuyến tính đơn giản (Simple Linear Regression) là chỉ có một biến đầu vào, và hồi quy tuyến tính đa biến (có nhiều biến đầu vào. Hồi quy tuyến tính là cần tìm các giá trị sao cho hàm mất mát MSE (Mean Squared Error) là nhỏ nhất.

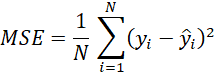
Trong đó  là giá trị thực tế,  là giá trị dự đoán, N là số lượng dữ liệu. Để tối ưu các tham số w, thuật toán thường sử dụng là phương pháp bình phương tối thiểu (Least Squares Method) hoặc Gradient Descent.

Cho một bài toán như sau: Một công ty bất động sản muốn xây dựng mo hình dự đoán giá nhà dựa trên diện tích. Dữ liệu lịch sử thu thập được từ 10 că nhà như sau:

Chúng ta sẽ sử dụng scikit-learn để huấn luyện mô hình. Bài toán chia làm 5 bước chính.

Bước 1: Import thư viện

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

from sklearn.model_selection import train_test_split

from sklearn.metrics import mean_squared_error, r2_score

Bước 2: Chuẩn bị dữ liệu

# Dữ liệu về diện tích và giá nhà

data = {

    ‘Diện tích (m2)’: [30, 50, 70, 90, 110, 130, 150, 170, 190, 210],

    ‘Giá nhà (triệu đồng)’: [1.5, 2.5, 3.5, 4.5, 5.0, 6.0, 6.8, 7.5, 8.5, 9.0]

}

# Chuyển thành DataFrame

df = pd.DataFrame(data)

# X là diện tích, y là giá nhà

X = df[[‘Diện tích (m2)’]]  # Chú ý: X phải là DataFrame

y = df[‘Giá nhà (triệu đồng)’]  # y là Series

# Chia dữ liệu thành tập huấn luyện (80%) và tập kiểm tra (20%)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Bước 3: Xây Dựng Mô Hình Hồi Quy Tuyến Tính

# Khởi tạo mô hình hồi quy tuyến tính

model = LinearRegression()

# Huấn luyện mô hình với tập dữ liệu huấn luyện

model.fit(X_train, y_train)

# Lấy hệ số hồi quy

w1 = model.coef_[0]  # Hệ số của diện tích (slope)

w0 = model.intercept_  # Hệ số chặn (intercept)

print(f’Phương trình hồi quy: y = {w0:.2f} + {w1:.2f} * X’)

Bước 4: Dự Đoán Giá Nhà Và Đánh Giá Mô Hình

# Dự đoán trên tập kiểm tra

y_pred = model.predict(X_test)

# Tính sai số MSE (Mean Squared Error)

mse = mean_squared_error(y_test, y_pred)

# Tính R² Score để đo độ chính xác

r2 = r2_score(y_test, y_pred)

print(f’Mean Squared Error (MSE): {mse:.4f}’)

print(f’R² Score: {r2:.4f}’)

Bước 5: Vẽ Biểu Đồ

plt.scatter(X, y, color=’blue’, label=’Dữ liệu thực tế’)

plt.plot(X, model.predict(X), color=’red’, label=’Hồi quy tuyến tính’)

plt.xlabel(‘Diện tích (m2)’)

plt.ylabel(‘Giá nhà (triệu đồng)’)

plt.title(‘Hồi Quy Tuyến Tính Dự Đoán Giá Nhà’)

plt.legend()

plt.show()

Kết quả là:

Phương trình hồi quy: y = 0.54 + 0.04 * X

Mean Squared Error (MSE): 0.0154

R² Score: 0.9983

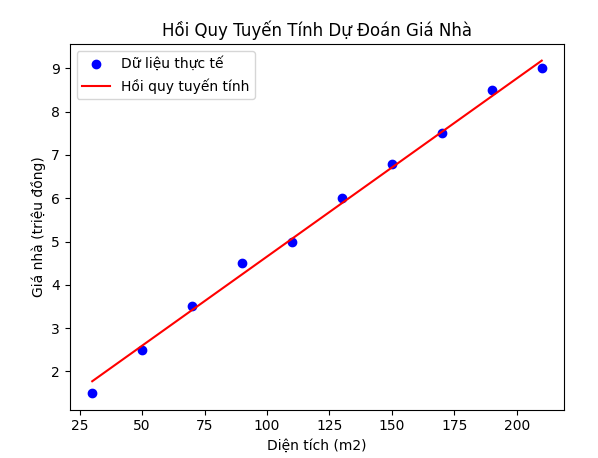
Ảnh 4‑1: Kết quả vẽ đồ thị của quá trình huấn luyện