itcctv_soft
17/07/2025
Bài toán balo (Knapsack)
Cho một tập hợp n đồ vật, mỗi đồ vật có trọng lượng wi và giá trị vi. Một ba lô có sức chứa tối đa W. Bài toán yêu cầu chọn các đồ vật vào balo sao cho tổng giá trị lớn nhất mà không vượt quá trọng lượng W.
Các thuật toán thường được sử dụng để giải quyết bài toán là quy hoạch động (giải bài toán bằng cách chia thành các bài toán con nhỏ hơn), thuật toán nhánh cận (tìm kiếm cắt tỉa để loại bỏ trường hợp không cần thiết), thuật toán di truyền (tối ưu hóa dựa trên chọn lọc tự nhiên).
Ứng dụng của bài toán này là quản lý tài nguyên, lập lịch, đóng gói hàng hóa, tối ưu hóa đầu tư tài chính.
Sau đây sử dụng thuật toán quy hoạch động để giải bài toán trên. Quy hoạch động (Dynamic Programming - DP) là một phương pháp tối ưu hóa dùng để giải các bài toán có tính chất chồng lặp và tối ưu con, bằng cách lưu trữ kết quả của các bài toán con để tránh tính toán lại.
Xét bài toán ba lô ở dạng bài toán ba lô 0/1 có nghĩa là mỗi vật phẩm chỉ được chọn tối đa 1 lần. Bài toán yêu cầu chọn một số vật phẩm từ danh sách nnn vật phẩm sao cho tổng giá trị là lớn nhất mà vẫn đảm bảo tổng trọng lượng không vượt quá giới hạn W.
Tính chồng lặp:
- Khi xét một vật phẩm, chúng ta có thể lựa chọn lấy nó hoặc bỏ qua.
- Quyết định tại vật phẩm thứ i có thể dẫn đến trạng thái giống như khi xét vật phẩm i −1 với một sức chứa khác.
- Ví dụ: Nếu ta đang xét vật phẩm thứ 3 và sức chứa còn lại là 1kg, kết quả của nó có thể giống như khi xét vật phẩm thứ 2 với sức chứa 1kg.
Tính tối ưu con:
- Nếu một lời giải tối ưu cho bài toán lớn bao gồm một bài toán con, thì bài toán con cũng phải có lời giải tối ưu.
- Nếu ta đã chọn vật phẩm i, bài toán con còn lại chính là bài toán chọn các vật phẩm trước đó với sức chứa bị giảm đi.
Xây dựng công thức truy hồi
Tại mỗi vật phẩm i, ta có hai lựa chọn:
- Không chọn vật phẩm i: Khi đó, giá trị tối ưu vẫn giữ nguyên như lúc xét i −1 vật phẩm với sức chứa w.
- Chọn vật phẩm i (nếu nó có thể đặt vào balo, tức là
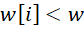) khi đó giá trị tối ưu là tổng của giá trị của vật phẩm i tức là 
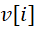và giá trị tối ưu của bài toán khi xét các vật phẩm trước đó và sức chứa giảm đi 
.
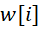Chọn giá trị lớn nhất giữa hai trường hợp:
Với điều kiện 
, nếu không thì 
Điều kiện biên
- Nếu không có vật phẩm nào (i=0) hoặc sức chứa bằng 0 (w=0), giá trị tối ưu là 0.
Ví dụ cho 3 vật phẩm có trọng lượng [1,2,3] và giá trị [6,10,12] và sức chứa của ba lô là W=5
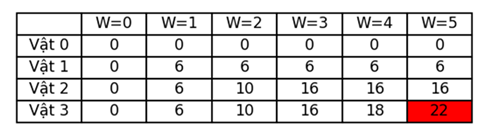
Ảnh 3‑12: Bảng giá trị dp chứa giá trị tối ưu tại mỗi giá trị W
Cài đặt thuật toán trên python:
def knapsack_traceback(W, weights, values, n):
# Khởi tạo bảng DP
dp = [[0 for _ in range(W + 1)] for _ in range(n + 1)]
# Tính toán bảng DP
for i in range(1, n + 1):
for w in range(W + 1):
if weights[i - 1] <= w:
dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1])
else:
dp[i][w] = dp[i - 1][w]
# Truy vết để tìm danh sách vật phẩm đã chọn
w = W
selected_items = []
for i in range(n, 0, -1):
if dp[i][w] != dp[i - 1][w]: # Nếu giá trị thay đổi, nghĩa là vật phẩm i đã được chọn
selected_items.append(i - 1)
w -= weights[i - 1] # Giảm sức chứa của balo
return dp[n][W], selected_items
# Ví dụ sử dụng
values = [6, 10, 12] # Giá trị của các vật phẩm
weights = [1, 2, 3] # Trọng lượng của các vật phẩm
W = 5 # Sức chứa balo
n = len(values)
max_value, items = knapsack_traceback(W, weights, values, n)
print("Giá trị lớn nhất có thể có:", max_value)
print("Các vật phẩm được chọn (chỉ số trong danh sách):", items)
print("Các vật phẩm được chọn (giá trị - trọng lượng):", [(values[i], weights[i]) for i in items])
Bình luận