Bài toán quy hoạch tuyến tính (Linear Programming)
Tối ưu hóa một hàm tuyến tính có dạng: max(hoặc min) c1x1 + c2x2 + …. + cnxn và có các ràng buộc tuyến tính:
a11x1 + a12x2 + …+ a1nxn <= b1
a21x1 + a22x2 + …+ a2nxn <= b2
Các thuật toán được sử dụng là thuật toán Simplex (giải quyết bài toán quy hoạch tuyến tính bằng cách đi qua các đỉnh của miền khả thi) và thuật toán nội điểm (tiếp cận nghiệm bên trong miền khả thi)
Ví dụ:
Một nhà máy cần tối ưu sản xuất hai sản phẩm A và B với:
- Mỗi sản phẩm mất số giờ sản xuất nhất định.
- Mỗi sản phẩm đem lại lợi nhuận khác nhau.
- Tài nguyên có giới hạn (ví dụ: số giờ tối đa trong một tuần).
Hàm mục tiêu có thể là tối đa hóa lợi nhuận: với ràng buộc:
Chúng ta sử dụng Thư viện scipy.optimize để giải bài toán này:
linprog(c, A_ub=A, b_ub=b, bounds=x_bounds, method='highs')
Hàm này tìm giá trị tối thiểu nên nếu tìm giá trị tối đa ta cần đổi chiều giá trị tham số từ dương sang âm.

Cài đặt trong python:
from scipy.optimize import linprog
# Hệ số của hàm mục tiêu (đảo dấu vì linprog mặc định là minimization)
c = [-5, -3]
# Hệ số của ràng buộc (bên trái dấu ≤)
A = [
[2, 1],
[1, 2]
]
b = [8, 6] # Giới hạn của ràng buộc (bên phải dấu ≤)
# Giới hạn của biến x1 và x2 (x1, x2 >= 0)
x_bounds = [(0, None), (0, None)]
# Giải bài toán
result = linprog(c, A_ub=A, b_ub=b, bounds=x_bounds, method="highs")
# Hiển thị kết quả
if result.success:
print("Giá trị tối đa của Z:", -result.fun)
print("Số lượng x1:", result.x[0])
print("Số lượng x2:", result.x[1])
else:
print("Không có lời giải tối ưu")
Kết quả là:

Ảnh 3‑13:Kết quả của quá trình tính giá trị tối ưu x1, x2 bằng quy hoạch tuyến tính
Nếu thể hiện vùng nghiệm trên đồ thị 2D ta có đồ thị sau:
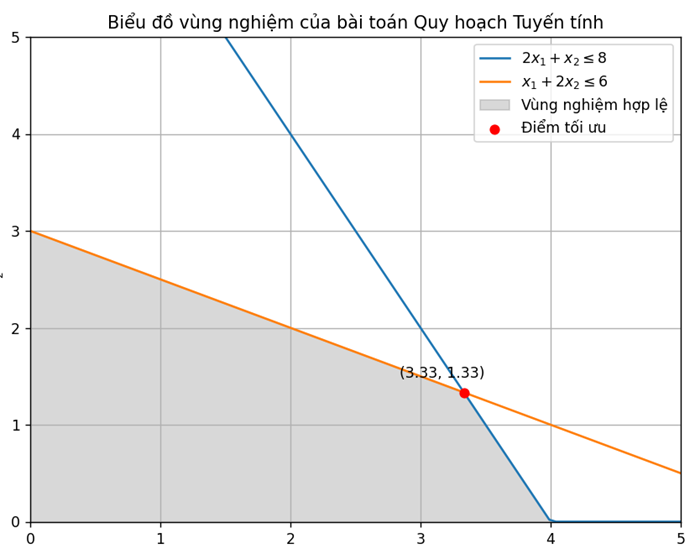
Ảnh 3‑14: Ví dụ thể hiện giá miền nghiệm trên đồ thị 2D
Đối với bài toán cần tối ưu với nhiều hơn 2 biến, việc thể hiện trên đồ thị rất khó khăn, nên sử dụng các hàm tối ưu hoá hiệu quả hơn rất nhiều.
Tài liệu đính kèm













Bình luận